
3èmes - Lundi 18 mai ~ vendredi 22 mai (2/2): fonctions linéaires
Résumé de la séance:
- reconnaitre si une fonction est linéaire (à partir de son expression, de sa représentation graphique ou d'un tableau de valeur)
- tracer la droite représentative d'une fonction linéaire
- pente d'une droite
a. La fonction \(f\) multiplie le nombre \(x\) par 4 (et c'est tout). C'est une fonction linéaire. b. La fonction \(g\) additionne 5 au nombre \(x\). Ce n'est pas une fonction linéaire. c. La fonction \(h\) multiplie le nombre \(x\) par 3 puis soustrait 5 au résultat. Ce n'est pas une fonction linéaire. d. La fonction \(k\) multiplie le nombre \(x\) par \(\frac{3}{7}\) (et c'est tout). C'est une fonction linéaire. 1. La représentation graphique est bien une droite qui passe par l'origine. C'est caractéristique d'une situation de proportionnalité. Elle représente donc une fonction linéaire. 2. La représentation graphique est bien une droite mais celle-ci ne passe pas par l'origine du repère. Cela implique que pour la fonction représentée, l'image de 0 n'est pas 0 (on peut lire que l'image de 0 est environ 0,5). Donc la fonction représentée ne peut pas être linéaire. C'est vrai qu'en français, "linéaire" fait penser à "droite"... Mais cela ne suffit pas... Rassurez-vous: nous verrons très bientôt ce type de fonction qui va aussi nous intéresser ! 1. Toutes ces fonctions sont des fonctions linéaires. Elles sont donc représentées par des droites qui passe par l'origine. Pour trouver ces droites, il nous faut donc uniquement trouver un autre point que l'origine qui en fasse partie. L'idée de l'exercice est que vous cherchiez à construire un tableau de valeurs (ou au moins chercher l'image d'un nombre différent de 0). Ce tableau permet d'obtenir 7 points de la droite (alors que 2 nous suffisent). En fait, nous savions déjà que le point de coordonnées (0;0) appartiendrait à la droite (c'est l'origine du repère). L'autre point pratique qui aurait suffit est le point de coordonnées \((1;3)\). Encore une fois, l'image de 1 nous aurait suffit à trouver le point de coordonnées \((1;-1)\). c. \(h : x \mapsto 1,5x\) cette fonction multiplie par 1,5 Pour cette fonction, suivant ce que nous avons choisit pour l'unité des axes du repère, cela peut être plus ou moins pratique d'utiliser le point de coordonnées (1;1,5). d. \(k : x \mapsto -\frac{2}{3}x\) cette fonction multiplie par \(-\frac{2}{3}\) Pour cette fonction, suivant ce que nous avons choisit pour l'unité des axes du repère, cela peut être plus ou moins pratique d'utiliser le point de coordonnées \((1;-\frac{2}{3})\). 2. En corrigeant la question 1, j'ai déjà répondu à celle-ci: J'ai rajouté le cas général en dernière ligne de ce tableau. Correction
3 p122: reconnaître si une fonction est linéaire à partir de son expression
4 p122: reconnaître si une fonction est linéaire à partir de sa représentation graphique
Pour prendre un peu d'avance sur la suite, on peut estimer visuellement que l'image de 2 est environ 1. On peut donc en déduire que la fonction représentée divise par 2, ce qui correspond à multiplie par 0,5.
La fonction linéaire représentée est donc \(x \mapsto 0,5x\).
Une fonction qui se contente de multiplier (par n'importe quel nombre) renvoit toujours 0 quand on lui "donne" 0 en entrée.
Pour n'importe quel nombre \(a\): \(0 \xrightarrow[~~~~~~~~~]{\times a} 0\) 6 p122: tracer la représentation graphique d'une fonction linéaire à partir de son expression
a. \(f : x \mapsto 3x\) cette fonction multiplie par 3
\(x\)
nombre de départ...
-3
-2
-1
0
1
2
3
...
\(f(x)\)
nombre d'arrivée lui correspondant...
-9
-6
-3
0
3
6
9
...
b. \(g : x \mapsto -x\) cette fonction multiplie par -1
\(x\)
...
-3
-2
-1
0
1
2
3
...
\(g(x)\)
...
3
2
1
0
-1
-2
-3
...
\(x\)
...
-3
-2
-1
0
1
2
3
...
\(h(x)\)
...
-4,5
-3
-1,5
0
1,5
3
4,5
...
On pourra donc lui préférer le point de coordonnées (2;3) pour avoir des coordonnées avec des nombres entiers.
\(x\)
...
-3
-2
-1
0
1
2
3
...
\(k(x)\)
...
\(-3\times -\frac{2}{3}=2\)
\(-2\times -\frac{2}{3}=\frac{4}{3}\)
\(-1\times -\frac{2}{3}=\frac{2}{3}\)
0
\(-\frac{2}{3}\)
\(2\times -\frac{2}{3}=\frac{-4}{3}\)
\(3\times -\frac{2}{3}=-2\)
...
On pourra donc lui préférer le point de coordonnées (3;-2) pour avoir des coordonnées avec des nombres entiers.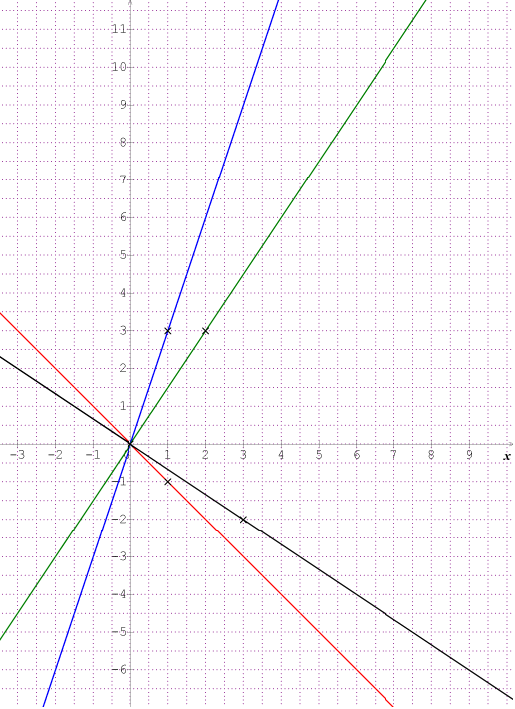
fonction
image de 1
\(f:x\mapsto 3x\)
3
\(g:x\mapsto -x\)
-1
\(h:x\mapsto 1,5x\)
1,5
\(k:x\mapsto -\frac{2}{3}x\)
\(-\frac{2}{3}\)
\(x\mapsto ax\)
a
En reprenant les tableaux de valeur du dernier exercices, vous pouvez vous rendre compte que ce sont en fait des "tables de mutiplications". exemple: Les autres exemples sont moins parlants car il n'est pas courant de faire des tables de "-1", de "1,5" et encore moins de "\(\frac{2}{3}\)" mais c'est le même principe. Je vais donc rester sur la fonction \(f:x \mapsto 3x\) pour la suite des explications. Si on prend un pas de 1 dans la première ligne ("on avance de 1 en 1"), alors la deuxième ligne "avance de 3 en 3". Allez sur l'application geogebra et faites varier la valeur du curseur \(a\). Vous verrez que la droite réagit au changement de valeur de \(a\). → quand on part d'un point de la droite, en avançant de 1 vers la droite puis de \(a\) vers le haut (ou vers le bas en fonction de son signe), on retombe sur un autre point de la droite. Le nombre \(a\) s'appelle la pente de la droite. C'est exactement la même notion que la pente d'une montagne que nous avions vu en trigonométrie. exemples: Le coefficient \(a\) dans l'expression \(x\mapsto ax\) s'appelle la pente de la droite représentative de cette fonction. Il indique si la droite monte ou descend, et à quelle vitesse. Cours
est la table de multiplication par 3
\(x\)
...
-3
-2
-1
0
1
2
3
...
\(f(x) = 3x\)
...
-9
-6
-3
0
3
6
9
...
Cela se retrouve sur le graphique: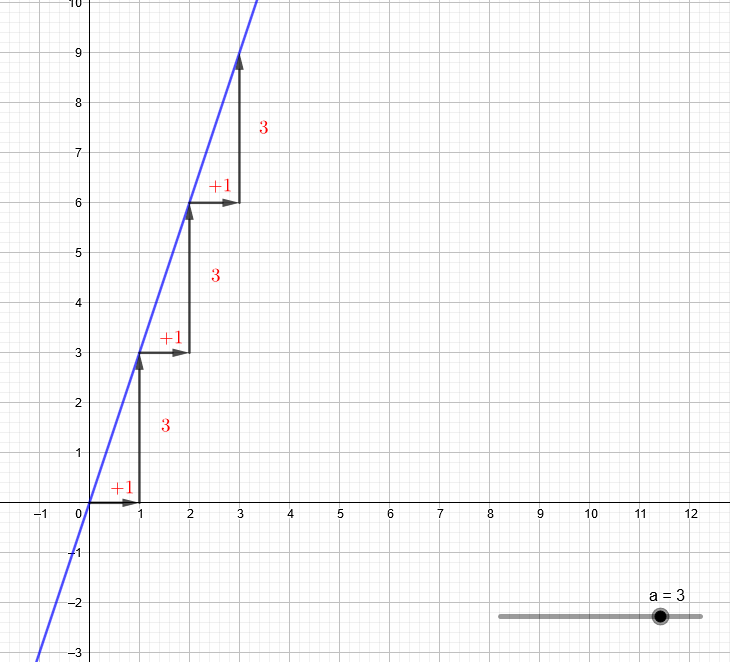
→ L'espèce d’escalier dessiné a des marche de la hauteur \(a\).
quand j'avance de 100 horizontalement, je monte (ou je descend) de 10 verticalement
quand j'avance de 1 horizontalement, je monte de 3 verticalement
quand j'avance de 3 horizontalement, je descend de 2 verticalement
On dit aussi "coefficient directeur".
A faire
Attention:
Certaines pentes de droites sont des fractions, essayez de vous inspirer de l'explication ci-dessus sur la pente d'une montagne et comparer "déplacement vertical / déplacement horizontal"
9 p123 trouver l'expression d'une fonction linéaire à partir de sa droite représentative
11 p123 même chose avec en plus des questions de lecture graphique
40 p127 trouver l'expression d'une fonction pour confirmer (ou non) une lecture graphique



